再帰処理を使って階乗の計算をしてみよう
まずは「再帰」と「階乗」の用語の確認からしましょう。
再帰とは
再帰(さいき)は、あるものについて記述する際に、記述しているものそれ自身への参照が、その記述中にあらわれることをいう。
うーん、むずかしいですね~
でも大丈夫です。もりさんがしっかり解説してくれますから
階乗とは
階乗とは、1~nまでの数字の積です。
n! = n × (n-1) ×・・・× 3 × 2 × 1
n=5の場合、
5!=5×4×3×2×1なので「5の階乗は120」となります。
コード
下記のコードをF8キーでステップ実行してみてください
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Sub main() Dim answer As Long answer = nの階乗(5) Debug.Print answer End Sub Function nの階乗(n As Long) As Variant If n = 1 Then nの階乗 = 1 Else nの階乗 = n * nの階乗(n - 1) End If Debug.Print n & "の階乗は" & nの階乗 End Function |
Functionプロシージャ nの階乗()の、この部分が再帰です。
nの階乗 = n * nの階乗(n - 1)
Function nの階乗() が、 Function nの階乗()に引数を渡して呼び出します
再帰のやさしい解説
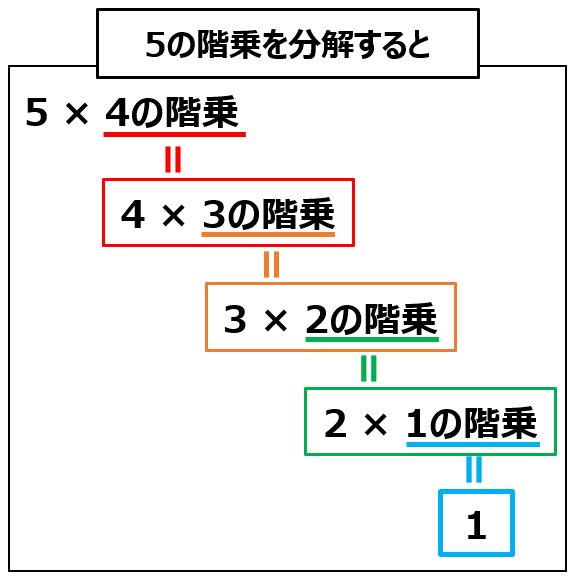
この図をみると、階乗の計算はこんな風に分解できますね。
- 5の階乗=5 × 4の階乗
- 4の階乗=4 × 3の階乗
- 3の階乗=3 × 2の階乗
- 2の階乗=2 × 1の階乗
- 1の階乗=1
これらの数字をすべてnに置き換えるとこのように書けます。
nの階乗=n × (n-1)の階乗
「呼び出す」と「返る」を理解する
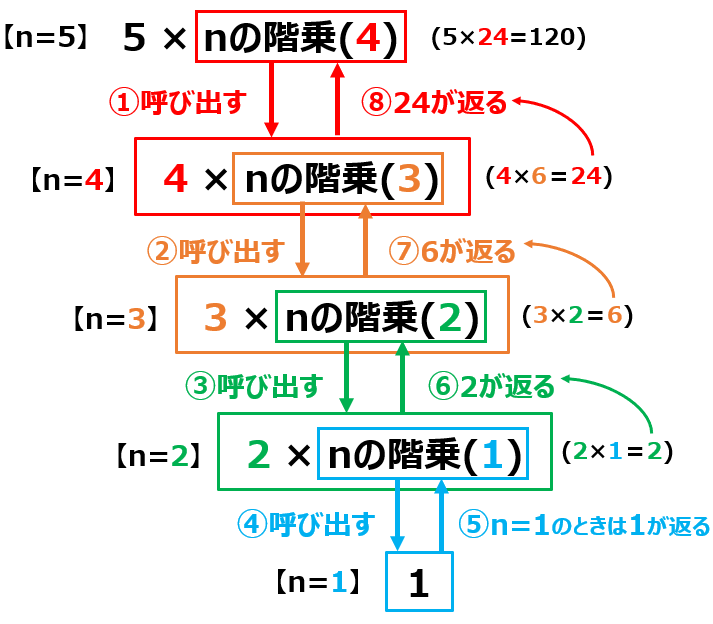

①[5の階乗]は5×[4の階乗]なので、[4の階乗]を求めるために、function nの階乗()に引数4を渡して呼び出す
②[4の階乗]は4×[3の階乗]なので、[3の階乗]を求めるために、function nの階乗()に引数3を渡して呼び出す
③[3の階乗]は3×[2の階乗]なので、[2の階乗]を求めるために、function nの階乗()に引数2を渡して呼び出す
④[2の階乗]は2×[1の階乗]なので、[1の階乗]を求めるために、function nの階乗()に引数1を渡して呼び出す
⑤[1の階乗]は “1”なので、呼び出し元に1を返す
⑥[2×1]=”2”なので、呼び出し元に2を返す
⑦[3×2]=”6”なので、呼び出し元に6を返す
⑧[4×6]=24なので、呼び出し元に24を返す
最後:[5×24]は120である
このように、
①呼び出す→②呼び出す→③呼び出す→④呼び出す→⑤返る→⑥返る→⑦返る→⑧返る
のイメージがつかめればバッチリです!