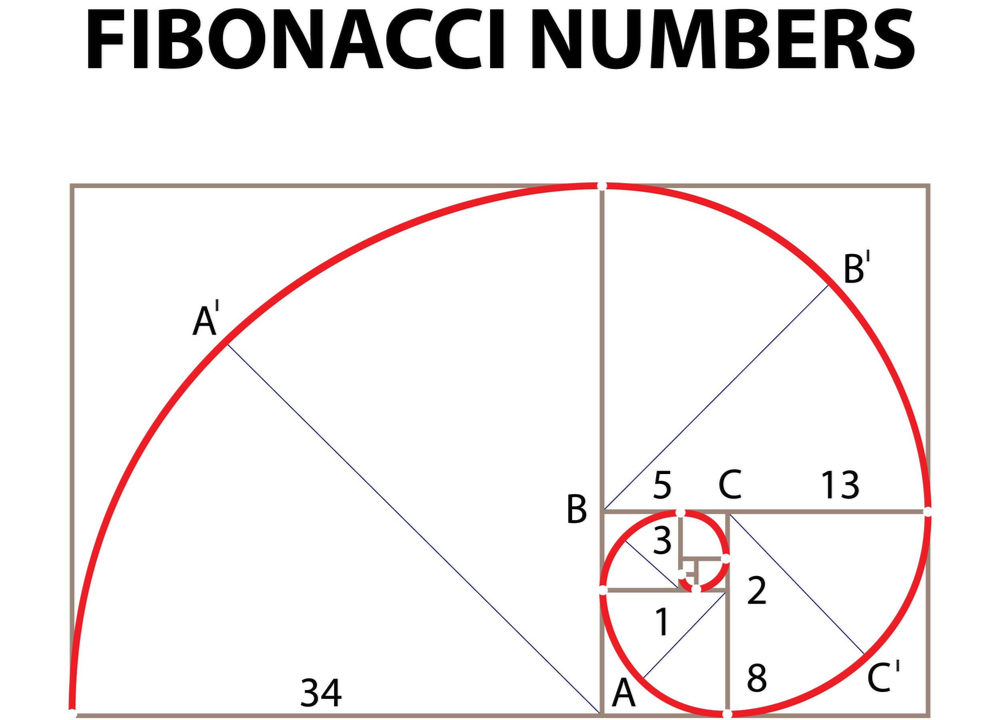
【再帰処理をマスターしよう】VBAでフィボナッチ数列を書いてみる

ねぇもりさん、今日学校で「フィボナッチ数列」を習ったよ

1,1,2,3,5,8って足してくやつ

もり

お～！それじゃあ、フィボナッチ数列をVBAで書いてみよっか！

ほら、このまえ勉強した再帰処理をつかってみよう

【再帰処理をマスターしよう】VBAで階乗の計算をしてみる自身への参照？呼び出す？返る？再帰処理ってむずかしいですよね。VBAで階乗の計算をして、再帰処理をマスターしてみよう！...

もりさん、グイグイくるね。まぁそういうとこキライじゃないよ

あっ、ちなみにひまわりの種の並びはフィボナッチ数列になっているそうですよ。

あとは、松ぼっくりとか、カタツムリの殻とか。

Contents

フィボナッチ数列とは？
VBAでフィボナッチ数列の第ｎ項を求める
- 再帰なしのパターン
- 再帰ありのパターン
再帰あり・なしの実行時間を比較してみた

フィボナッチ数列とは？

第１項＝１・第２項＝１として、【２つ前の数字】と【１つ前の数字】の合計を並べたものです。

１，１，２，３，５，８，１３，２１，３４，５５・・・

※ネットで色々みると、フィボナッチ数列の第１項は０と書いてあったり、１と書いてあったりします。

この記事では第１項＝１としてプログラムを実装します。

VBAでフィボナッチ数列の第ｎ項を求める

「再帰あり」と「再帰なし」の２パターンで書いてみました。

再帰なしのパターン

Sub フィボナッチ数を求める_再帰なし()

    Dim x As Variant '第n項の2つ前の値
    Dim y As Variant '第n項の1つ前の値
    
    x = 1 '第1項の値
    y = 1 '第2項の値
    
    '★★★求めたい項を指定★★
    Dim n As Long: n = 10
    
    '計算回数をカウント※第1,2項の値はセットしているので、第3項から計算開始
    Dim cnt As Long: cnt = 3
    
    Do While cnt <= n
    
        Dim total As Variant
        total = x + y
        
        x = y
        y = total
            
        cnt = cnt + 1
        
    Loop
    
    '★★★答え★★★
    Debug.Print "第" & n & "項→" & total

End Sub

Sub フィボナッチ数を求める_再帰なし()

Dim x As Variant '第n項の2つ前の値

Dim y As Variant '第n項の1つ前の値

x = 1 '第1項の値

y = 1 '第2項の値

'★★★求めたい項を指定★★

Dim n As Long: n = 10

'計算回数をカウント※第1,2項の値はセットしているので、第3項から計算開始

Dim cnt As Long: cnt = 3

Do While cnt <= n

Dim total As Variant

total = x + y

x = y

y = total

cnt = cnt + 1

Loop

'★★★答え★★★

Debug.Print "第" & n & "項→" & total

End Sub

Do～Loop文でやってることはこんな感じです。

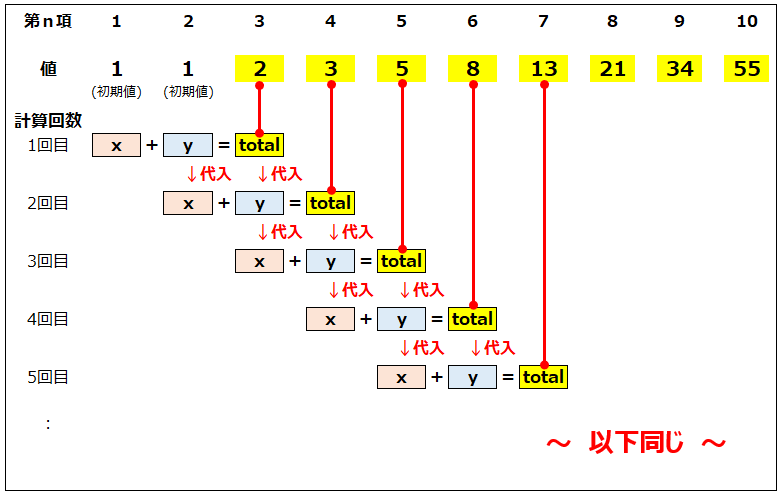
桁あふれを考慮して、x,y,totalはVariant型にしています。

第50項だと12,586,269,025になるんですね！

再帰ありのパターン

Sub フィボナッチ数を求める_再帰あり()
    
    '★★★求めたい項を指定★★
    Dim n As Long: n = 10

    Dim total As Variant
    total = Fib(n)
    
    Debug.Print "第" & n & "項→" & total

End Sub

Function Fib(n As Long) As Variant

    If n = 1 Or n = 2 Then
        Fib = 1
    Else
        Fib = Fib(n - 2) + Fib(n - 1)
    End If

End Function

Sub フィボナッチ数を求める_再帰あり()

'★★★求めたい項を指定★★

Dim n As Long: n = 10

Dim total As Variant

total = Fib(n)

Debug.Print "第" & n & "項→" & total

End Sub

Function Fib(n As Long) As Variant

If n = 1 Or n = 2 Then

Fib = 1

Else

Fib = Fib(n - 2) + Fib(n - 1)

End If

End Function

Function Fib() が　Function Fib()を呼び出していますね。

Fib(10) = Fib(8) + Fib(9)

【２つ前の値】と【１つ前の値】の合計値を求めるので、第１０項＝第８項＋第９項となります。

再帰あり・なしの実行時間を比較してみた

「再帰処理はメモリを食うから遅くなる」といった話を聞いたので、実験してみました。

第20項あたりから差がつくようです。

第n項	再帰なし	再帰あり	計算結果
20	0.001~2秒	0.004秒	6,765
25	〃	0.023秒	75,025
30	〃	0.216秒	832,040
35	〃	2.29秒	9,227,465
36	〃	3.772秒	14,930,352
37	〃	6.145秒	24,157,817
38	〃	9.934秒	39,088,169
39	〃	16.065秒	63,245,986
40	〃	26.358秒	102,334,155
45	〃	応答なし	1,134,903,170
50	〃	やめておく	12,586,269,025